Constructing the model in the 2D space
1. Compute hexagonal grid configurations
Number of bins along the x-axis
To begin the algorithm, you need to determine the number of bins along the x-axis for creating regular hexagons in the hexagonal grid.
num_bins_x <- calculate_effective_x_bins(.data = UMAP_data, x = UMAP1,
cell_area = 1)
num_bins_x
#> [1] 6Shape parameter
Then, you need to determine the shape parameter, which control the shape and size of the hexagons in the hexagonal grid.
shape_value <- calculate_effective_shape_value(.data = UMAP_data,
x = UMAP1, y = UMAP2)
shape_value
#> [1] 2.0194142. Obtain hexagonal bin centroids
hexbin_data_object <- extract_hexbin_centroids(nldr_df = UMAP_data,
num_bins = num_bins_x, shape_val = shape_value)
df_bin_centroids <- hexbin_data_object$hexdf_data
df_bin_centroids
#> # A tibble: 27 × 5
#> x y hexID counts std_counts
#> <dbl> <dbl> <int> <int> <dbl>
#> 1 -2.32 -5.74 2 4 0.667
#> 2 -2.79 -4.92 8 3 0.5
#> 3 -1.84 -4.92 9 5 0.833
#> 4 -3.27 -4.09 15 5 0.833
#> 5 -2.32 -4.09 16 1 0.167
#> 6 -1.36 -4.09 17 2 0.333
#> 7 -2.79 -3.26 22 2 0.333
#> 8 -1.84 -3.26 23 1 0.167
#> 9 -0.885 -3.26 24 2 0.333
#> 10 -0.407 -2.44 32 1 0.167
#> # ℹ 17 more rows
hexbin_object <- hexbin_data_object$hb_data
str(hexbin_object)
#> Formal class 'hexbin' [package "hexbin"] with 16 slots
#> ..@ cell : int [1:27] 2 8 9 15 16 17 22 23 24 32 ...
#> ..@ count : int [1:27] 4 3 5 5 1 2 2 1 2 1 ...
#> ..@ xcm : num [1:27] -2.37 -2.8 -1.8 -3.01 -2.76 ...
#> ..@ ycm : num [1:27] -5.61 -5.08 -5.03 -3.97 -4.06 ...
#> ..@ xbins : num 6
#> ..@ shape : num 2.02
#> ..@ xbnds : num [1:2] -3.27 2.46
#> ..@ ybnds : num [1:2] -5.74 5.82
#> ..@ dimen : num [1:2] 16 7
#> ..@ n : int 75
#> ..@ ncells: int 27
#> ..@ call : language hexbin::hexbin(x = dplyr::pull(nldr_df, { { ...
#> ..@ xlab : chr [1:5] "dplyr::pull(nldr_df, {" " {" " x" " }" ...
#> ..@ ylab : chr [1:5] "dplyr::pull(nldr_df, {" " {" " y" " }" ...
#> ..@ cID : int [1:75] 15 54 62 2 23 104 54 39 54 97 ...
#> ..@ cAtt : int(0)3. Remove low-density hexagons
## To identify low density hexagons
df_bin_centroids_low <- df_bin_centroids |>
dplyr::filter(std_counts <= 0.1666667)
## To identify low-density hexagons needed to remove by investigating neighbouring mean density
identify_rm_bins <- find_low_density_hexagons(df_bin_centroids_all = df_bin_centroids, num_bins_x = num_bins_x, df_bin_centroids_low = df_bin_centroids_low)
## To remove low-density hexagons
df_bin_centroids <- df_bin_centroids |>
dplyr::filter(!(hexID %in% identify_rm_bins))4. Triangulate hexagonal bin centroids
Next, you need to perform triangulation on the bin centroids to construct a triangular mesh. Triangulation involves connecting the bin centroids with triangular edges to form a mesh that reveals the local structure of the data.
tr1_object <- triangulate_bin_centroids(.data = df_bin_centroids, x = x, y = y)
str(tr1_object)
#> List of 10
#> $ n : int 26
#> $ x : num [1:26] -2.32 -2.79 -1.84 -3.27 -2.32 ...
#> $ y : num [1:26] -5.74 -4.92 -4.92 -4.09 -4.09 ...
#> $ tlist: int [1:144] 3 2 1 3 2 -1 -4 4 5 1 ...
#> $ tlptr: int [1:144] 2 7 4 9 6 18 1 3 8 11 ...
#> $ tlend: int [1:26] 7 4 6 91 17 20 45 30 36 41 ...
#> $ tlnew: int 131
#> $ nc : num 0
#> $ lc : num 0
#> $ call : language tripack::tri.mesh(x = dplyr::pull(.data, { { ...
#> - attr(*, "class")= chr "tri"
tr_from_to_df <- generate_edge_info(triangular_object = tr1_object)
tr_from_to_df
#> # A tibble: 65 × 6
#> from to x_from y_from x_to y_to
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 3 -2.32 -5.74 -1.84 -4.92
#> 2 1 2 -2.32 -5.74 -2.79 -4.92
#> 3 2 5 -2.79 -4.92 -2.32 -4.09
#> 4 2 3 -2.79 -4.92 -1.84 -4.92
#> 5 3 6 -1.84 -4.92 -1.36 -4.09
#> 6 4 5 -3.27 -4.09 -2.32 -4.09
#> 7 4 7 -3.27 -4.09 -2.79 -3.26
#> 8 5 6 -2.32 -4.09 -1.36 -4.09
#> 9 6 14 -1.36 -4.09 1.02 0.0427
#> 10 6 9 -1.36 -4.09 -0.407 -2.44
#> # ℹ 55 more rows## To draw the traingular mesh
trimesh <- ggplot(df_bin_centroids, aes(x = x, y = y)) +
geom_trimesh() +
coord_equal() +
xlab(expression(C[x]^{(2)})) + ylab(expression(C[y]^{(2)})) +
theme(axis.text = element_text(size = 5),
axis.title = element_text(size = 7))
trimesh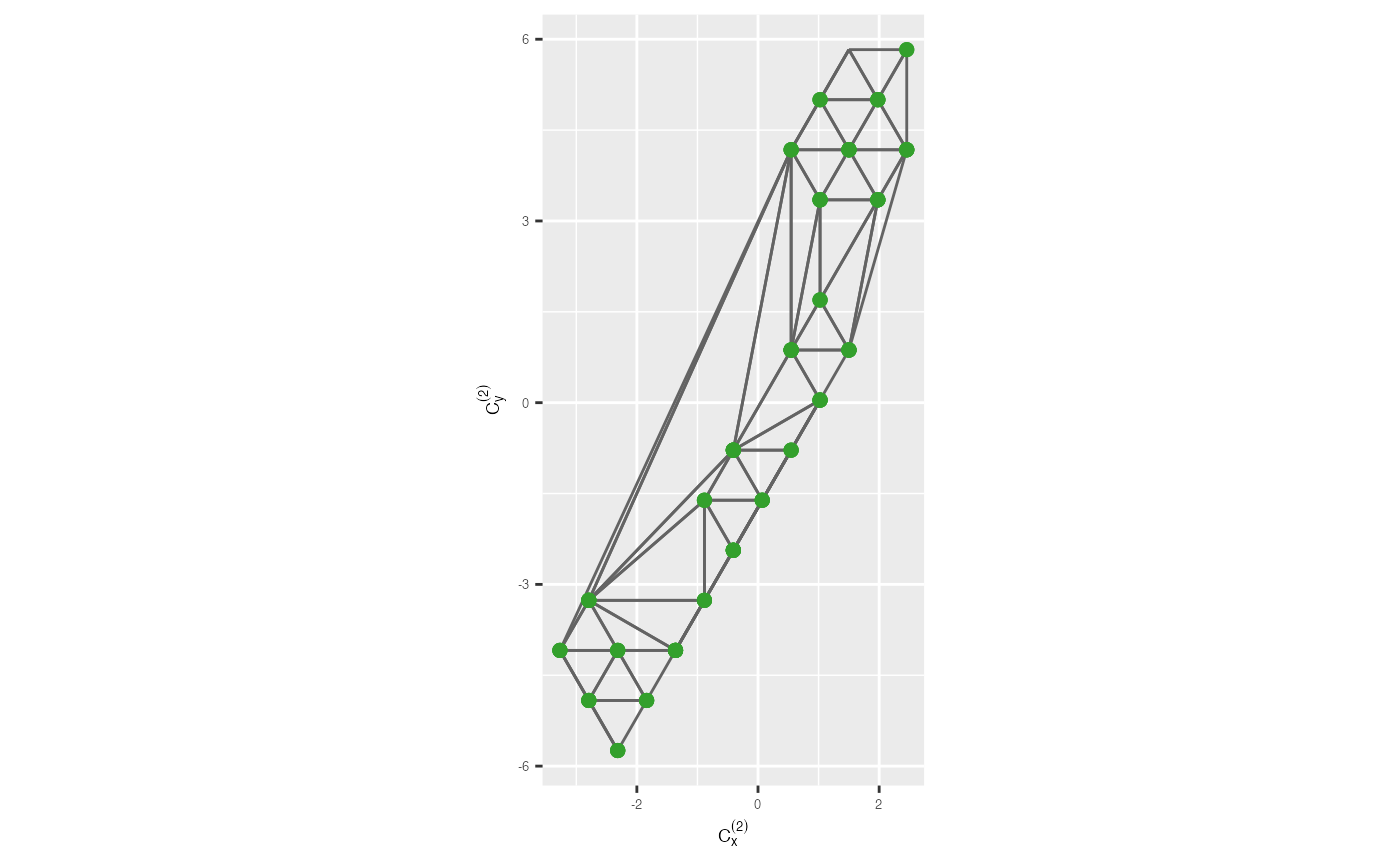
5. Remove long edges
## Compute 2D distances
distance <- cal_2d_dist(.data = tr_from_to_df)
## To find the benchmark value to remove long edges
benchmark <- find_benchmark_value(.data = distance, distance_col = distance)
benchmark
#> [1] 1.653## To draw the traingular mesh after remove long edges in 2D
trimesh_removed <- remove_long_edges(.data = distance, benchmark_value = benchmark,
triangular_object = tr1_object, distance_col = distance) +
xlab(expression(C[x]^{(2)})) + ylab(expression(C[y]^{(2)})) +
theme(axis.text = element_text(size = 5),
axis.title = element_text(size = 7))
trimesh_removed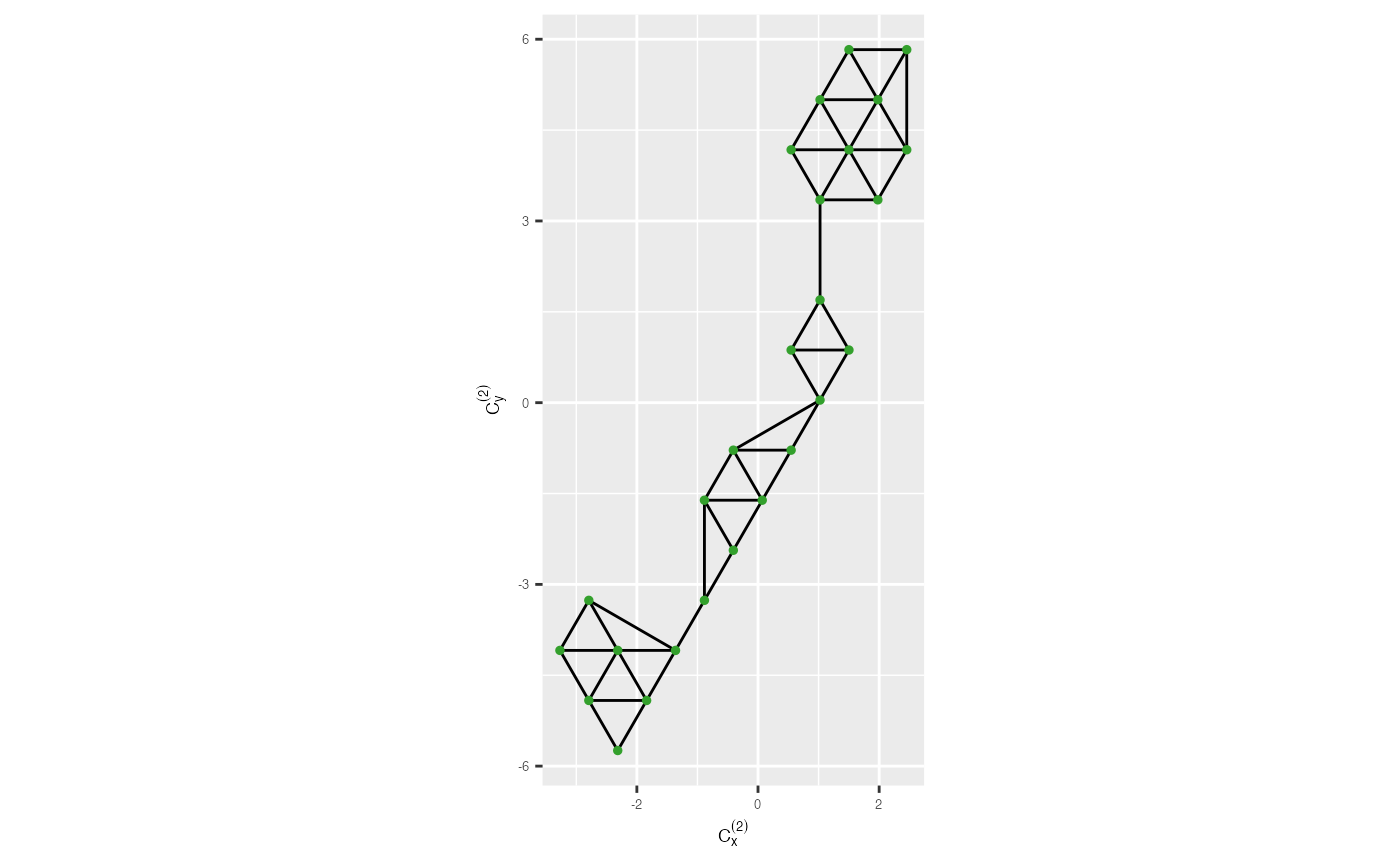
Lifting the model into high dimensions
To extend the model created in the 2D space to higher dimensions, you need to take the average of the high-dimensional coordinates within hexagonal bins.
## Add hexbin Ids for the 2D embeddings
UMAP_data_with_hb_id <- UMAP_data |>
dplyr::mutate(hb_id = hexbin_data_object$hb_data@cID)
UMAP_data_with_hb_id
#> # A tibble: 75 × 4
#> UMAP1 UMAP2 ID hb_id
#> <dbl> <dbl> <int> <int>
#> 1 -2.81 -3.91 1 15
#> 2 0.959 -0.00271 2 54
#> 3 1.54 0.462 3 62
#> 4 -2.31 -5.50 4 2
#> 5 -1.76 -3.46 6 23
#> 6 1.53 5.75 7 104
#> 7 0.930 -0.175 8 54
#> 8 0.319 -1.61 9 39
#> 9 1.37 0.0541 11 54
#> 10 1.90 4.94 12 97
#> # ℹ 65 more rows
## To generate a data set with high-dimensional training data and 2D embeddings with hexagonal IDs
df_all <- dplyr::bind_cols(training_data |> dplyr::select(-ID), UMAP_data_with_hb_id)
df_all
#> # A tibble: 75 × 11
#> x1 x2 x3 x4 x5 x6 x7 UMAP1 UMAP2
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 -0.120 0.114 -1.99 -0.00246 -0.0178 -0.0181 -3.17e-3 -2.81 -3.91
#> 2 -0.0492 0.822 0.00121 0.0161 0.00968 -0.0834 2.30e-3 0.959 -0.00271
#> 3 -0.774 0.243 0.367 -0.0198 0.00408 -0.0349 -9.11e-3 1.54 0.462
#> 4 -0.606 1.96 -1.80 0.0132 -0.000479 -0.00478 -8.43e-3 -2.31 -5.50
#> 5 0.818 0.0388 -1.58 0.00253 0.00167 0.0781 -7.71e-3 -1.76 -3.46
#> 6 0.910 1.55 1.42 0.0124 0.0160 -0.00248 -8.32e-3 1.53 5.75
#> 7 -0.0691 0.978 0.00239 0.0115 0.00350 0.0898 3.59e-3 0.930 -0.175
#> 8 0.859 1.55 -0.488 -0.00753 -0.0123 0.0336 -6.65e-3 0.319 -1.61
#> 9 -0.0400 0.286 0.000801 0.0123 0.00613 -0.0121 -3.47e-4 1.37 0.0541
#> 10 0.765 0.898 1.64 -0.0178 0.0151 -0.0710 -6.24e-3 1.90 4.94
#> # ℹ 65 more rows
#> # ℹ 2 more variables: ID <int>, hb_id <int>
df_bin <- avg_highD_data(.data = df_all)
df_bin
#> # A tibble: 27 × 8
#> hb_id x1 x2 x3 x4 x5 x6 x7
#> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 2 -0.637 1.74 -1.76 0.00953 -0.00143 -0.0117 -0.00152
#> 2 8 -0.727 1.07 -1.43 0.00721 0.0138 -0.0529 -0.000473
#> 3 9 0.171 1.56 -1.93 0.00613 -0.00726 -0.0212 -0.00198
#> 4 15 -0.424 0.196 -1.86 -0.00854 -0.00598 -0.0195 0.00165
#> 5 16 -0.186 0.532 -1.98 0.0189 0.00972 -0.0112 -0.00900
#> 6 17 0.603 1.00 -1.77 0.0158 -0.00995 0.00976 0.000755
#> 7 22 0.0548 0.0438 -1.96 0.00858 0.0115 -0.0317 -0.00197
#> 8 23 0.818 0.0388 -1.58 0.00253 0.00167 0.0781 -0.00771
#> 9 24 0.943 0.757 -1.32 -0.00720 -0.00319 0.0572 0.00230
#> 10 32 0.988 0.673 -0.848 0.0177 -0.00890 0.0114 0.00460
#> # ℹ 17 more rowsVisualize the model and high-dimensional data in the high-dimensional space
To visualize the model and the high-dimensional data, tour technique is used.
tour1 <- show_langevitour(df_all, df_bin, df_bin_centroids, benchmark_value = benchmark,
distance = distance, distance_col = 'distance')
tour1